神经网络

摘要

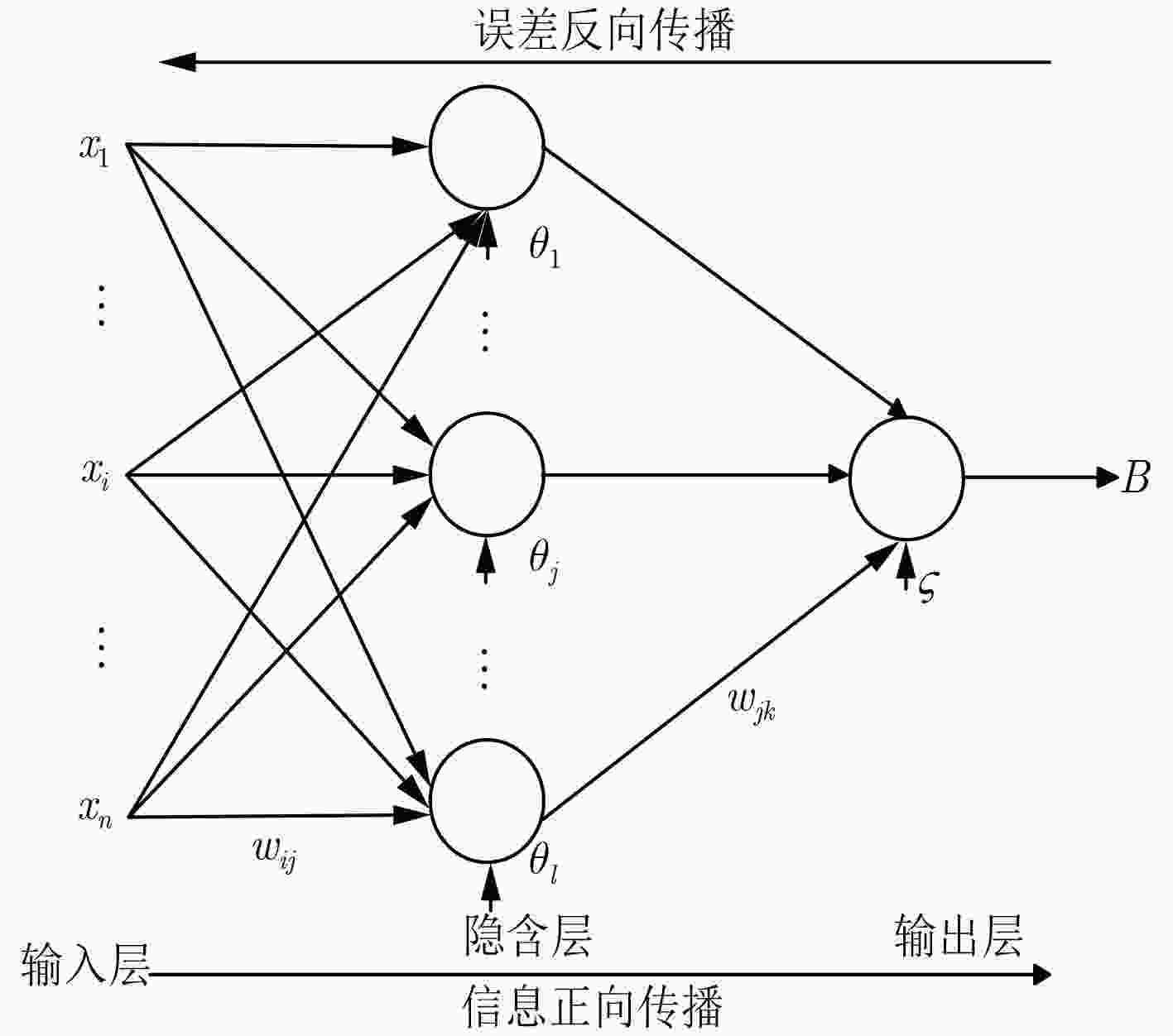
神经网络可以说是目前人工智能算法中应用最为广泛的算法之一，相比Linear regression 、logistics regression、decision tree等机器学习算法等会复杂不少，变化也很多。本文从向量矩阵的角度去理解BP神经网络的数学原理，这个过程会显得更加清晰、简洁。我们以最经典的神经网络三层网络二分类模型为例，逐步推导数学公式，三层网络简单说明如下：

输入层，不做处理，只是输入数据
$n_h$ 我们就以RELU为激活函数，另外一个常用的是sigmoid，我们把激活函数封装成一个类，可以随时替换
输出层为一个单元，由于是二分类，我们就用sigmoid拟合对应类1的概率

符号定义

$X$ $Y$ $Y$ $m\times 1$ 的矩阵。
$m$ $n$ 为样本向量的维度。
$f$ $f_h$ $f_h(x) = max(0, x)$ $f_o$ $f_o(x) = \frac{1}{1+exp(-x)}$
$Y_h$ $Y_o$
$w_h$ $N_h$ $W_h$ $w_o$ $N_o$ $W_o$ 。
$Yo$ $W_o$ 表示，从而使得算法是通用的，改成onehot+softmax方式的多分类，也是适用的。
$Y_o = f_o(f_h(X \cdot W_h) \cdot Wo)$
$X \cdot W_h$ $X$ 增加一个全1的列，达到同样的效果。

forward公式推导

\begin{align} x_{hj} &= x_i \cdot w_{hj} \\ y_{hj} &= f_h(x_{hj}) \\ x_o &= y_{hj} \cdot w_{o} \\ y_{o} &= f_o(x_o) \\ \end{align}

\begin{align} X_h &= X \cdot W_h \\ Y_h &= f_h(X_h) \\ X_o &= Y_h \cdot W_o \\ Y_o &= f_o(X_o) \\ &= f_o(Y_h \cdot W_o) \\ &= f_o(f_h(X_h) \cdot W_o) \\ &= f_o(f_h(X \cdot W_h) \cdot Wo) \tag{1} \end{align}

其中（1）式即为信息正向传导的向量化公式相应的python代码实现：


#forward
Lh = np.dot(X, Wh)
Yh = funcActivation.cal(Lh) #隐藏层输出
Yh = np.insert(Yh, np.shape(Yh)[1], values=np.ones(m), axis=1)#add all 1 col
Lo = np.dot(Yh, Wo)
Yo = funcOut.cal(Lo)

其中 funcActivation 为隐藏层激活函数的封装，这里使用的Relu，funcOut为输出层激活函数的封装，使用的是sigmoid。


xxxxxxxxxx
class ReLU:
    def cal(self, z):
        return np.clip(z, 0, np.inf)
    def grad(self, x):
        return (x > 0).astype(int)
class Sigmoid:
    def cal(self, z):
        return 1 / (1 + np.exp(-z))
    def grad(self, x):
        z = self.cal(x)
        return z*(1-z)

损失函数

最常用的有Mean Square Error均方差损失函数，用于分类的Cross Entropy等。本文以经典的MSE为例。如下（2）式是MSE损失函数的向量化表示。

\begin{align} e &= \frac{1}{2m}\sum_{i=1}^{m} (y_{oi} - y_i)^2 \\ &= \frac{1}{2m}(Y_o - Y)^T \cdot (Y_o - Y) \tag{2} \\ \end{align}

误差反向传播

我们目的是最小化损失函数，通常使用梯度下降法，逐渐逼近最小极值点。需要逐渐求解参数主要是两个：

$W_h$ $W_o$ ,下面分别计算对应损失函数的偏导数。

\begin{align} \mathrm{d}e &= \frac{1}{2m}tr((\mathrm{d}Y_o)^T \cdot (Y_o - Y) + (Y_o - Y)^T \cdot \mathrm{d}Y_o) \\ &= \frac{1}{2m}tr((\mathrm{d}Y_o)^T \cdot (Y_o - Y)) + \frac{1}{2m}tr((Y_o - Y)^T \cdot \mathrm{d}Y_o) \\ &= \frac{1}{2m}tr(\mathrm{d}Y_o \cdot (Y_o - Y)^T) + \frac{1}{2m}tr((Y_o - Y)^T \cdot \mathrm{d}Y_o) \\ &= \frac{1}{m}tr((Y_o - Y)^T \cdot \mathrm{d}Y_o) \tag{3} \\ &= \frac{1}{m}tr((Y_o - Y)^T \cdot (f_o^{'}(X_o) \odot \mathrm{d}X_o)) \tag{4} \\ &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot \mathrm{d}X_o) \tag{5} \\ &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot (Y_h \cdot \mathrm{d}W_o + \mathrm{d}Y_h \cdot W_o)) \tag{6}\\ \end{align}

$tr(A^T) = tr(A)$ $tr(A^T \cdot (B \odot C)) = tr((A \odot B)^T \cdot C)$ $\odot$ $W_o$ $Y_h$ $\mathrm{d}Y_h$ 忽略，继续推导：

\begin{align} \mathrm{d}e &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot (Y_h \cdot \mathrm{d}W_o)) \\ &= \frac{1}{m}tr((Y_h^T \cdot ((Y_o - Y) \odot f_o^{'}(X_o)))^T \cdot \mathrm{d}W_o) \tag{7} \\ \frac{\partial e}{\partial W_o} &= \frac{1}{m}Y_h^T \cdot ((Y_o - Y) \odot f_o^{'}(X_o)) \tag{8} \\ \end{align}

$\mathrm{d}f = tr((\frac{\partial f}{\partial x})^T \mathrm{d}x)$ 的性质。对应python实现：


xxxxxxxxxx
delta = np.multiply(self.lossFunc.grad(Yo, Y) , funcOut.grad(Lo))
dO  = np.dot(Xo.T, delta)

$\frac{\partial e}{\partial W_h}$ ：

\begin{align} \mathrm{d}e &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot (\mathrm{d}Y_h \cdot W_o)) \tag{9} \\ &= \frac{1}{m}tr(W_o \cdot ((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot \mathrm{d}Y_h ) \\ &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T)^T \cdot \mathrm{d}Y_h ) \\ &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T)^T \cdot (f_h^{'}(X_h) \odot \mathrm{d}X_h) ) \\ &= \frac{1}{m}tr((((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h))^T \cdot \mathrm{d}(X_h) ) \tag{10} \\ &= \frac{1}{m}tr((((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h))^T \cdot \mathrm{d}(X \cdot W_h) ) \\ &= \frac{1}{m}tr((X^T \cdot (((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h)))^T \cdot \mathrm{d}W_h ) \\ \frac{\partial e}{\partial W_h} &= \frac{1}{m}X^T \cdot (((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h)) \tag{11}\\ \end{align}

对应的python的实现：


xxxxxxxxxx
delta = np.multiply(self.lossFunc.grad(Yo, Y) , funcOut.grad(Lo))
dH = np.dot(X.T, np.multiply(np.dot(delta, Wo.T[:,:-1]) , funcActivation.grad(Lh)))

$b$ 的数学推导

$X$ $b$ ,下面再推导一下使用偏置的方式

\begin{align} x_{hj} &= x_i \cdot w_{hj} + b_{hj} \\ y_{hj} &= f_h(x_{hj}) \\ x_o &= y_{hj} \cdot w_{o} + b_{oj} \\ y_{o} &= f_o(x_o) \\ \end{align}

\begin{align} X_h &= X \cdot W_h + B_h \\ Y_h &= f_h(X_h) \\ X_o &= Y_h \cdot W_o + B_o \\ Y_o &= f_o(X_o) \\ &= f_o(Y_h \cdot W_o + B_o) \\ &= f_o(f_h(X_h + B_h) \cdot W_o + B_o) \\ &= f_o(f_h(X \cdot W_h+ B_h) \cdot Wo + B_o) \tag{12} \end{align}

\begin{align} de &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot \mathrm{d}X_o) \tag{5} \\ &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot \mathrm{d}(Y_h \cdot W_o + B_o)) \\ &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot (\mathrm{d}(Y_h \cdot W_o) + \mathrm{d}B_o)) \\ \end{align}

$\frac{\partial e}{\partial W_o}$ $\frac{\partial e}{\partial B_o}$ :

\begin{align} de &= \frac{1}{m}tr(((Y_o - Y) \odot f_o^{'}(X_o))^T \cdot \mathrm{d}B_o) \\ \frac{\partial e}{\partial W_o} &= \frac{1}{m}Y_h^T \cdot ((Y_o - Y) \odot f_o^{'}(X_o)) \tag{8} \\ \frac{\partial e}{\partial B_o} &= \frac{1}{m}(Y_o - Y) \odot f_o^{'}(X_o) \end{align}

$\frac{\partial e}{\partial W_o}$ $\frac{\partial e}{\partial B_h}$ :

\begin{align} de &= \frac{1}{m}tr((((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h))^T \cdot \mathrm{d}(X_h) ) \tag{10} \\ &= \frac{1}{m}tr((((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h))^T \cdot \mathrm{d}(X \cdot W_h + B_h) ) \\ \end{align}

$\frac{\partial e}{\partial W_h}$ $\frac{\partial e}{\partial B_o}$ :

\begin{align} de &= \frac{1}{m}tr((((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h))^T \cdot \mathrm{d}(X_h) ) \tag{10} \\ &= \frac{1}{m}tr((((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h))^T \cdot \mathrm{d}B_h ) \\ \frac{\partial e}{\partial W_h} &= \frac{1}{m}X^T \cdot (((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h)) \tag{11}\\ \frac{\partial e}{\partial B_h} &= \frac{1}{m}((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T) \odot f_h^{'}(X_h)\\ \end{align}

总结

多层网络
本文实现的是基于输入层、隐藏层、输出层经典的三层神经网络架构，在此基础上可以实现更多隐藏层的神经
网络。我们观察隐藏层的参数基于损失函数的偏导（11）式与输出层的（8）式区别：
$\begin{align} \frac{\partial e}{\partial W_h} &= X^T \cdot (\overbrace{\frac{1}{m}((Y_o - Y) \odot f_o^{'}(X_o) \cdot W_o^T)}^{\delta_o} \odot f_h^{'}(X_h)) \nonumber\\ \frac{\partial e}{\partial W_o} &= Y_h^T \cdot (\overbrace{\frac{1}{m}(Y_o - Y)}^{\delta} \odot f_o^{'}(X_o)) \nonumber \end{align}$
$\frac{\partial e}{\partial W_h}$ $X^T$ 项是自己这一层的输入，
$\delta_o$ $\frac{\partial e}{\partial W_h}$
$\delta$ 为损失函数的导数，我们可以把他看成输出层的上一层的反馈值，所以
每层的参数矩阵的偏导可以统一公式为:
$\begin{align} \frac{\partial e}{\partial W_{i}} = X_i^T \cdot (\delta_{i+1} \odot f_i^{'}(X_i \cdot W_i)) \nonumber \end{align}$
linear regression
如果把隐藏层去掉，输出层的激活函数也去掉，那么只有一层的神经网络就是多元线性回归。
$\begin{align} Y = X \cdot w + b \nonumber \end{align}$
Logistics regression
如果把隐藏层去掉，输出层的激活函数使用sigmoid，那么只有一层的神经网络就是就变成了逻辑回归。
$\begin{align} Y = \frac{1}{1+exp(X \cdot w + b)} \nonumber \end{align}$
关于隐藏层数量的选择
有一些启发式的公式选择隐藏层数量，但是主要还是通过实验选择最恰当的参数，这里可以使用交叉验证的
方式。如将训练样本3/7分割为验证数据集和训练数据集，然后先从少的隐藏层数量开始试，选择在训练
数据集上拟合效果好，同时在验证数据集上同样具有接近准确度的参数作为最终参数结果。

程序实现

使用python库sklearn自带的数据集breast_cancer，共569行数据，30个维度。完整python实现代码:


x
import numpy as np 
from sklearn import datasets
from sklearn.datasets import load_breast_cancer
from sklearn import preprocessing
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score
dataset = None
DT_FLAG = 1 #1测试预测，2测试回归拟合
if DT_FLAG:
    dataset = load_breast_cancer()
else:
    dataset = datasets.load_boston()
class ReLU:
    def __init__(self):
        return
    def cal(self, z):
        return np.clip(z, 0, np.inf)
    def grad(self, x):
        return (x > 0).astype(int)
class Sigmoid:
    def __init__(self):
        return
    def cal(self, z):
        return 1 / (1 + np.exp(-z))
    def grad(self, x):
        z = self.cal(x)
        return z*(1-z)
class LossMSE:
    def __init__(self):
        return
    def loss(self, y_pred, y):
        return np.sum(np.multiply((y_pred - y) , (y_pred - y))) / 2 /int(y.shape[0]) 
    def grad(self, y_pred, y):
        return (y_pred - y)/y.shape[0]
class LossCrossEntropy:
    def loss(self, y_pred, y):
        eps = np.finfo(float).eps
        cross_entropy = -np.sum(y * np.log(y_pred + eps))
        return cross_entropy
    def grad(self, y_pred, y):
        grad = y_pred - y
        return grad
class LinearOut:#如果用于回归，只是线性输出，不做任何转换，是的可以有统一的结构
    def cal(self, z):
        return z
    def grad(self, x):
        self.gradCache = np.ones(np.shape(x))
        return self.gradCache
class NN:
    def __init__(self):
        self.Wh = None #隐藏层参数w
        self.Wo = None #输出层参数w
        self.numHideUnit = 5
        self.funcActivation = ReLU() #隐藏层激活函数
        if DT_FLAG:
            self.lossFunc = LossMSE()
            self.funcOut = Sigmoid()
        else:
            self.lossFunc = LossMSE()
            self.funcOut = LinearOut()
        return
    def fit(self, X, Y):
        scalerX = preprocessing.StandardScaler().fit(X)#StandardScaler
        Y = Y.reshape(-1, 1)
        X = scalerX.transform(X)
        if not DT_FLAG:
            scalerY = preprocessing.StandardScaler().fit(Y)#MinMaxScaler
            Y = scalerY.transform(Y)
        m, n = np.shape(X)
        funcActivation = self.funcActivation
        funcOut = self.funcOut 
        # 10 1000 0.01 for breat cancer
        numLayerHide = 5
        maxIterTimes = 2000 
        eta  = 0.01
        if DT_FLAG:
            eta  = 10
        else:
            #maxIterTimes = 100000
            eta  = 0.001#eta  = 0.00001
            pass
        outputNodeNum = 1
        Wh = np.random.rand(n, numLayerHide) * 0.01 
        Bh = np.random.rand(numLayerHide) * 0.01 
        Wo = np.random.rand(numLayerHide, outputNodeNum) * 0.01 #Why +1? for reserver b 
        Bo = np.random.rand(outputNodeNum) * 0.01 
        errLog = []
        dO_Old = 0
        dH_Old = 0
        for i in range(maxIterTimes):
            #forward
            Lh = np.dot(X, Wh) + Bh            
            Yh = funcActivation.cal(Lh) #隐藏层输出
            Lo = np.dot(Yh, Wo) + Bo
            Yo = funcOut.cal(Lo)
            loss = self.lossFunc.loss(Yo, Y)
            errLog.append(loss)
            if loss < 0.001:
                print('fit finish', i)
                break
            
            delta = np.multiply(self.lossFunc.grad(Yo, Y) , funcOut.grad(Lo))
            dBo  = delta
            dWo  = np.dot(Yh.T, dBo)
            
            dBh = np.multiply(np.dot(delta, Wo.T) , funcActivation.grad(Lh))
            dWh = np.dot(X.T, dBh)
            Wo = Wo - eta * dWo
            Wh = Wh - eta * dWh
            Bo = Bo - eta * dBo
            Bh = Bh - eta * dBh
            
        score = 0
        if DT_FLAG == 0:
            score = r2_score(Yo, Y)
        else:
            score = r2_score((Yo > 0.5).astype(int), Y)
        print('score', score)
        return
    if __name__ == '__main__':
        nn = NN()
        print('data', dataset.data.shape)
        nn.fit(dataset.data, dataset.target)