摘要
支持向量机(support vector machines, SVM)是一种分类模型,该模型在特征空间中求解间隔最大的分类超平面。当训练数据近似线性 可分时,可以通过增加软间隔学习一个线性分类器。当线性不可分时,利用核技巧,隐式的将特征空间映射到高维特征空间,从而达到线性 可分。使用序列最小最优化算法(SMO),可以快速求解模型的参数。 关键字:支持向量机; SVM; SMO; 矩阵运算; 矩阵求导;numpy;sklearn.
数学推导与python实现
SVM简介
当训练数据线性可分,可以得到一个线性超平面 ,将在超平面上方的归为正类,将在超平面下方的归为负类。当数据点 与超平面距离越远时,表示分类的确定性越高,这样虽然线性分类的超平面可能有无数多个,但是我们可以找到一个所有点距离超平面最大的一个 超平面。相应的决策函数为:

最大间隔分类超平面
为正时,为正,当 为负时,为负,则可以定义 为几何间隔,表示数据点距离超平面的距离。 模型最终会找到一个参数为和的分离超平面,所有点距离超平面的距离都大于等于d,将距离正好等于d的数据点称之为支持向量。
将 和 进行一定比例的缩放
可以{eq1}将式化简为:
将{eq2} 和 {eq3} 利用拉格朗日乘数法,获得拉格朗日原始问题形式:
当满足KTT条件时, 拉格朗日对偶问题的解等价于{eq4} 的解:
求解拉格朗日对偶问题
首先求L以 w、b为参数的极小值,通过求微分得到偏导数形式。
从而得到w、b 偏导数,并令偏导数为0。
推导出如下关系:
将{eq6}式 和 {eq7}式 代入{eq5}式中,
去除负号,将极大转换成极小形式:
为了使拉格朗日对偶问题的解与原始问题解相同,需要同时满足KTT条件:
软间隔
当训练数据近似线性可分,有些异常点或噪声点导致无法找到分离超平面,可以对每个数据点加一个松弛变量,从而让所有数据点均满足约束。
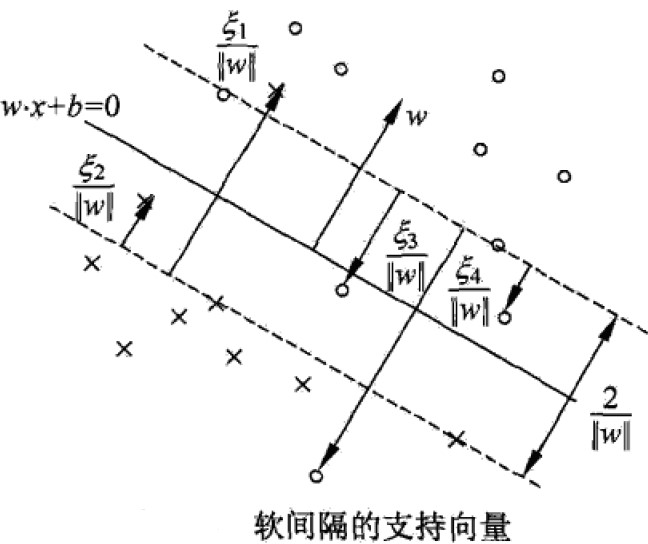
加入软间隔参数,每个向量点距离分类超平面距离增加,同时增加一个惩罚系数C,代入{eq5}新形式如下:
将其转换为拉格朗日对偶形式:
求得对于w、b、 的偏导并令其为0:
代入 {eq9} 式中:
、 、约束可以化简为:
为了使拉格朗日对偶问题的解与原始问题解相同,需要同时满足KTT条件:
核函数
近似线性可分用软间隔方式解决,然而当训练数据是非线性数据,会出现无法在原特征空间找到分离超平面。可以使用一个非线性变换,将数据从原特征空间映射到更高维的新空间,然后在新空间中寻找线性分类超平面,这种方法被称为核技巧。观察 {eq10} 式中计算,即需要计算 内积。将核技巧应用到SVM,定义核函数为:
即将原来的向量内积,改成先让向量映射到新空间,然后再求内积。核技巧的另外一个优点是,不需要显示的定义 而是直接计算出 的结果,以高斯核函数为例:
则 {eq10} 式利用核技巧转化为:
序列最小最优化算法SMO
支持向量机的拉格朗日对偶问题是一个凸二次规划问题,具有全局最优解,序列最小最优化算法即SMO算法,是高效求解支持向量机解的一种算法。其基本思路是,如果所有变量都满足了KTT条件,那么就求得了问题的解。SMO算法过程如下:
- 选择两个变量,如,固定其他变量,那么原问题就变成了两个变量的二次优化问题。
- 由于有约束的存在,选择了两个变量,实际上自由变量只有一个。
- 求解两个变量的最优解,迭代直到所有变量满足KTT条件。
- 迭代求解使用的解析方法,效率高
当选择两个变量,如时,将其他变量看做常数:
则上式子去除不包含 的项后化简为:
利用约束 得到:
将代入:
针对求导,并令导数为0:
则可以推得:
考虑到 令 ,将将内积转换成核函数形式,并且定义函数为函数与的误差值:
则 {eq12} 式得到未经剪辑的解为:
因为有约束 并且 ,下面讨论的上限下限,当时:
当时:
则经剪辑后解为:
对于偏置,由于KTT条件约束有:
对于任一有 整理后得到,当时:
当时:
若 、都满足条件,那么。当所有满足KTT条件时,模型得解。
总结
线性可分支持向量机
当训练数据线性可分时,支持向量机可以得到一个最大间隔的分离超平面,若近似可分,则可以添加软间隔的方式,若线性不可分,则可以利用核技巧确保可以找到最大间隔分离超平面。由于得到的分离间隔最大,支持向量机有较好的鲁棒性。
模型训练
通过拉格朗日对偶变换,通过KTT条件,可以将原始问题转换为拉格朗日对偶问题,从而自然的引入核函数。SMO是常用的模型训练算法,其本质上是凸二次规划问题,当所有变量都满足KTT条件,可以得到最佳解。SMO的计算过程直接利用解析解,求解速度较快。
参考文献
[1] Ian Goodfellow / Yoshua Bengio / Aaron Courville . Deep Learning[M]. 北京: 清华 大学出版社,2017-08-01. [2] 张贤达. 矩阵分析与应用[M]. 北京: 人民邮电出版社,2013-11-01. [3] 李航. 统计学习方法[M]. 北京: 清华大学出版社,2012-03. [4] David C. Lay / Steven R. Lay / Judi J. McDonald . 线性代数及其应用[M]. 北京: 机械工业出版社,2018-07. [5] 史蒂文·J. 米勒. 普林斯顿概率论读本[M]. 北京: 人民邮电出版社,2020-08.
支持向量机的python 源码
xxxxxxxxxx# -*- coding: utf8 -*-import mathimport timeimport numpy as np import sklearnfrom sklearn import datasetsfrom sklearn.datasets import load_breast_cancerfrom sklearn import preprocessingimport matplotlib.pyplot as pltfrom sklearn.metrics import r2_scoredataset = sklearn.datasets.load_breast_cancer()dataset.target[dataset.target == 0] = -1 #0/1 标记替换成1/-1标记class GSKernal: def __init__(self): self.sigma = 10 def cal(self, x, z): result = None if len(x.shape) == 2: result = np.linalg.norm(x-z, axis=1) ** 2 else: result = np.linalg.norm(x-z) ** 2 return np.exp(-1 * result / (2 * self.sigma**2))class SVM: def __init__(self, kn = None, C = 1, toler = 0.001): self.w = None #w self.b = None #b if not kn: kn = GSKernal() self.kn= kn self.C = C self.toler = toler self.alpha = None self.X = None self.Y = None self.kCache = {} return def calK(self, i, j): key = '' if i <= j: key = '%d_%d'%(i, j) else: key = '%d_%d'%(j, i) ret = self.kCache.get(key) if ret: return ret x1 = self.X[i] x2 = self.X[j] ret = self.kn.cal(x1, x2) self.kCache[key] = ret return ret def calK2(self, j): key = 'All_%d'%(j) ret = self.kCache.get(key) if ret: return ret['data'] ret = np.zeros(self.X.shape[0]) x2 = self.X[j] for i in range(self.X.shape[0]): x1 = self.X[i] ret[i] = self.kn.cal(x1, x2) self.kCache[key] = {'data':ret} return ret def isZero(self, v): return math.fabs(v) < self.toler def calGxi(self, i): xi = self.X[i] ay = np.multiply(self.alpha, self.Y) gxi = np.dot(ay, self.calK2(i)) + self.b return gxi def calcEi(self, i): gxi = self.calGxi(i) return gxi - self.Y[i] def isSatisfyKKT(self, i): gxi = self.calGxi(i) yi = self.Y[i] if self.isZero(self.alpha[i]) and (yi * gxi >= 1): return True elif self.isZero(self.alpha[i] - self.C) and (yi * gxi <= 1): return True elif (self.alpha[i] > -self.toler) and (self.alpha[i] < (self.C + self.toler)) \ and self.isZero(yi * gxi - 1): return True return False def getAlphaJ(self, E1, i): E2 = 0 maxE1_E2 = -1 maxIndex = -1 for j in range(self.X.shape[0]): if j == i: continue E2_tmp = self.calcEi(j) if E2_tmp == 0: continue if math.fabs(E1 - E2_tmp) > maxE1_E2: maxE1_E2 = math.fabs(E1 - E2_tmp) E2 = E2_tmp maxIndex = j if maxIndex == -1: maxIndex = i while maxIndex == i: maxIndex = int(random.uniform(0, self.X.shape[0])) E2 = self.calcEi(maxIndex) return E2, maxIndex def fit(self, X, Y, iterMax = 10): self.kCache.clear() scalerX = sklearn.preprocessing.StandardScaler().fit(X)#StandardScaler #Y = Y.reshape(-1, 1) X = scalerX.transform(X) w = np.zeros(X.shape[1]) self.b = 0 a = np.zeros(X.shape[0]) self.alpha = a self.X = X self.Y = Y iterStep = 0; parameterChanged = 1 calTims = 0 while (iterStep < iterMax) and (parameterChanged > 0): iterStep += 1 parameterChanged = 0 for i in range(self.X.shape[0]): if self.isSatisfyKKT(i): continue E1 = self.calcEi(i) E2, j = self.getAlphaJ(E1, i) y1 = self.Y[i] y2 = self.Y[j] x1 = self.X[i] x2 = self.X[j] a1_old = a[i] a2_old = a[j] if y1 != y2: L = max(0, a2_old - a1_old) H = min(self.C, self.C + a2_old - a1_old) else: L = max(0, a2_old + a1_old - self.C) H = min(self.C, a2_old + a1_old) if L == H: continue k11 = self.calK(i, i) k12 = self.calK(i, j) k21 = k12 k22 = self.calK(j, j) ay = np.multiply(a, self.Y) ayk1 = np.dot(ay, self.calK2(i)) ayk2 = np.dot(ay, self.calK2(j)) a2_new = a2_old + (y2 * (ayk1 - y1 - (ayk2 - y2))) / (k11 - 2*k12 + k22) a1_new = a1_old + y1 * y2 * (a2_old - a2_new) b1New = -1 * E1 - y1 * k11 * (a1_new - a1_old) \ - y2 * k21 * (a2_new - a2_old) + self.b b2New = -1 * E2 - y1 * k12 * (a1_new - a1_old) \ - y2 * k22 * (a2_new - a2_old) + self.b bNew = 0 if (a1_new > 0) and (a1_new < self.C): bNew = b1New elif (a2_new > 0) and (a2_new < self.C): bNew = b2New else: bNew = (b1New + b2New) / 2 self.alpha[i] = a1_new self.alpha[j] = a2_new self.b = bNew if math.fabs(a2_new - a2_old) >= 0.00001: parameterChanged += 1 calTims += 1 if calTims % 50 == 0: print('train iter:%d SMO times:%d'%(iterStep, calTims)) #time.sleep(1) #return Yo = self.predict(self.X) #print(Yo) score = r2_score(Yo, self.Y) print('score', score) return def predict(self, X): if len(X.shape) == 1: return self.predictOne(X) ret = np.zeros(X.shape[0]) for i in range(X.shape[0]): ret[i] = self.predictOne(X[i]) return ret def predictOne(self, x): ret = np.zeros(self.X.shape[0]) x2 = x for i in range(self.X.shape[0]): x1 = self.X[i] ret[i] = self.kn.cal(x1, x2) ay = np.multiply(self.alpha, self.Y) gxi = np.dot(ay, ret) + self.b if gxi > 0: return 1 return -1if __name__ == '__main__': svm = SVM() print('data', dataset.data.shape) svm.fit(dataset.data, dataset.target)