概念介绍：
继上篇贝叶斯后，一直想完成隐马尔科夫这篇，一是一直没有时间完成python的示例实现代码， 二是想找一个区别于天气的隐马尔科夫例子。区别于贝叶斯，隐马尔科夫模型是基于时序的概率模型， 本文只关注于一阶隐马尔科夫模型，即某一时刻的状态值只跟上一时刻的状态值有关。 该模型可以用三元组表示：λ = (A, B,π ), 其中：
- A：为状态转移概率矩阵
- B：为观察概率矩阵，或称为概率矩阵
- π：为初始概率矩阵
举一个例子来说明。
- 假设有一只电动玩具狗，它只会干三件事：汪汪叫（W），跑来跑去（R），睡觉（S）。则观察状态集合V为{W, R, S}, 则观察状态数目M=3 .
- 经过了解得知，电动玩具狗是受情绪控制的，它会无聊（B），高兴（H），生气（A），故状态集合Q={B, H，A}, 状态数目N=3
- 分析这只玩具狗后得知其状态转移概率矩阵为：
混淆矩阵为：
初始概率矩阵为：π = (0.2, 0.4, 0.4)
维特比算法
假设一天中观察到玩具狗的行为序列为{W,R,S,R,S}, 求最可能的情绪状态序列是什么。这是典型的隐马尔科夫解码问题，下面使用维特比算法求解。
维特比变量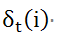
: 使t时刻为状态i的最佳状态序列的概率值,递推公式：
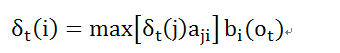
辅助变量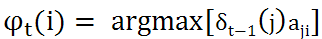
表示t时刻为状态i时的前一时刻t-1时的最佳状态，注意，
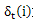为t时刻为i的最佳的概率，而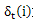为最佳状态值，
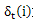由此也可知 记录了到达此点的最佳上一个时刻的状态点路径，故分配T*N数组存储，
用于最后回溯路径得到最终结果，动态规划的思想。
Python 实现代码：
class yieldmrkf_t:
def __init__(self, A, B, Pi, OSet, QSet):
self.A = A # 转移概率矩阵
self.B = B # 混淆概率矩阵
self.Pi = Pi # 初始概率矩阵
self.N = len(Pi) # 隐状态数量
self.M = len(B) / self.N # 观察状态数量
self.OsetVal = OSet
self.QSetVal = QSet
self.QSet = []
self.Oset = []
for i in range(0, self.N):
self.QSet.append(i)
for i in range(0, self.M):
self.Oset.append(i)
def dump(self):
strA = "A:"
i = 0
for k in self.A:
if i % self.N == 0:
strA = strA + "\n"
strA = strA + " " + str(k)
i = i + 1
print(strA)
i = 0
strB = "B:"
for k in self.B:
if i % self.M == 0:
strB = strB + "\n"
strB = strB + " " + str(k)
i = i + 1
print(strB)
print("Pi:", self.Pi, "N:", self.N, "M:", self.M)
def get_a(self, i, j):
return self.A[i*self.N + j]
def get_b(self, o, i):
return self.B[i*self.M + o]
def get_delta(self, delta_set, t, i):
return delta_set[t*self.N + i]
def convertOState(self, OStateSet_Val):
dest = []
for k in OStateSet_Val:
for i in range(0, self.M):
if k == self.OsetVal[i]:
dest.append(i)
return dest
def decode(self, OStateSet_Val):
OStateSet = self.convertOState(OStateSet_Val)
T = len(OStateSet)
# 初始化t= 1 的情况
delta_set = []
fai_set = []
for i in self.QSet:
delta_1_i = self.Pi[i] * self.get_b(OStateSet[0], i)
delta_set.append(delta_1_i)
fai_set.append(0)
# 递推求的delta 和fai
for t in range(1, T):
for i in self.QSet:
fai_t_i = 0
tmp_fai_i = 0
tmp_delta = 0
for j in self.QSet:
#compute fai
tmp = self.get_delta(delta_set, t - 1, j) * self.get_a(j, i)
if tmp > tmp_fai_i:
tmp_fai_i = tmp
fai_t_i = j
#compute delta
tmp = tmp * self.get_b(OStateSet[t], i)
if tmp > tmp_delta:
tmp_delta = tmp
fai_set.append(fai_t_i)
delta_set.append(tmp_delta)
#select last i
tmp_rate_i_T = 0
i_T = 0
for i in self.QSet:
tmp = self.get_delta(delta_set, T-1, i)
if tmp > tmp_rate_i_T:
tmp_rate_i_T = tmp
i_T = i
i_dest = []
i_dest.append(i_T)
for tmp_t in range(1, T):
t = T - tmp_t
i_dest.append(fai_set[(t) * self.N + i_dest[len(i_dest) - 1]])
dest = []
for n in range(0, T):
dest.append(self.QSetVal[i_dest[(T-n) - 1]])
return dest
OSet = ['W', 'R', 'S']
QSet = ['B','H', 'A']
O = ['W', 'R', 'S', 'R', 'S']
A = [0.5, 0.2, 0.3, 0.3, 0.5, 0.2, 0.2, 0.3, 0.5]
B = [0.5, 0.2, 0.3, 0.4, 0.1, 0.5, 0.7, 0.1, 0.2]
Pi = [0.2, 0.4, 0.4]
o = yieldmrkf_t(A, B, Pi, OSet, QSet)
o.dump()
dest = o.decode(O)
print("output:", dest
输出结果：
A:
0.5 0.2 0.3
0.3 0.5 0.2
0.2 0.3 0.5
B:
0.5 0.2 0.3
0.4 0.1 0.5
0.7 0.1 0.2
('Pi:', [0.2, 0.4, 0.4], 'N:', 3, 'M:', 3)
('output:', ['A', 'H', 'H', 'H', 'H'])
总结
- 隐马尔科夫适用于时序概率模型，“隐”的含义是既可观察的状态序列和隐藏（不可观察的）状态序列存在一定关系
- 本文探究了隐马尔科夫的解码问题，分析实现了维特比算法
- 隐马尔科夫的概率计算问题和模型参数学习问题待以后探究。
- 更多精彩文章 http://h2cloud.org